MAXA関数ではなく、MAX関数を使うべき

はじめに

先日『【MAX関数】使い方と解説 – 最大値 –』にて、MAX関数を取り上げました。
本記事では、MAX関数の姉妹関数であるMAXA関数を取り上げ、その違い、注意点をお伝えします。

MAX関数 -日付や時刻の平均値も算出できる- DL可

Excelの表計算を行う際に必要不可欠な関数の一つであるMAX関数。この関数は、引数として指定された数値の中から最大値を取得することができます。本記事では、MAX関数の基…

データ分析ドットコム

MAX関数

MAX関数は、数値の中で最大値を求める関数です。
文字列、論理値、空白のセルは計算対象外となります（見かけ上は0が返る）。

基本的な使い方は以下の通りです。

=MAX(数値1, 数値2,・・・) 

例えば、A1からA10までのセル範囲の最大値を求める場合は、以下のように入力します。

=MAX(A1:A10) 

「数値」「論理値」「空白セル」「文字列」が引数のMAX関数の戻り値

C列には、各行のA列とB列を引数としたMAX関数が入力されています。

「論理値」「空白セル」「文字列」を引数とした、C列の関数結果は、いずれも -1 が返ってきています。

行6のエラー値はエラーが返ってきています。
MAX関数の場合は、0が返ってきますが、計算対象ではありません。

次の表を確認ください。

「数値」「論理値」「空白セル」「文字列」を混在した引数のMAX関数の計算結果

先程の「論理値」「文字列」「空白セル」は0が返ってくることは確認しました。

各行のA列とB列を範囲指定したMAX関数がC列に入力されています。

A列「数値」、B列「論理値」or「文字列」or「空白セル」を比較すると、
MAX関数の結果は、いずれも 最大値 -1 です。

「論理値」「文字列」「空白セル」は0が返ってくるため、MAX関数では計算対象外であることが分かります。

なぜならば、「論理値」「文字列」「空白セル」がMAX関数の計算対象であれば、A列の -1 の方が小さくなるため、C列は0が表示されるはずだからです。

つまり、MAX関数の戻り値は、計算対象外となり、見かけ上0になっていることが分かります。

しかし、

MAXA関数は、「論理値」「文字列」「空白セル」の戻り値を計算対象になる性質を持っています。
つまり、C列の結果が、MAXA関数の場合、0になります。

具体的に、MAXA関数を次の表で見てみましょう。

MAXA関数

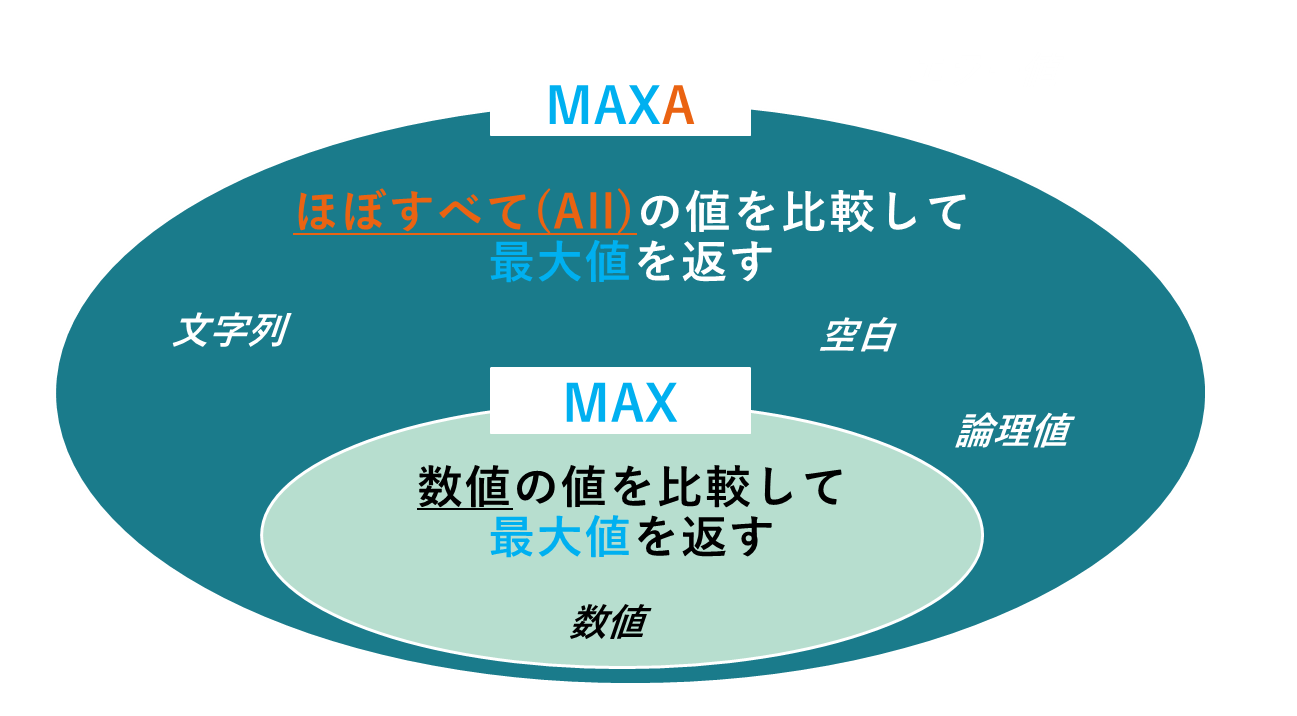
MAXA関数は、ほぼ全てデータの中で最大値を求める関数です。
まさに、名前の由来が「MAX All」たるゆえんです。

ほぼ全ての記載したのは、エラー値が対象外のためです
（エラー値を引数に取ると、エラーが返ってきます）

基本的な使い方は、MAX関数と同様で、以下の通りです。

=MAXA(数値1, 数値2,・・・) 

例えば、A1からA10までのセル範囲の最大値を求める場合は、以下のように入力します。

=MAXA(A1:A10) 

MAX関数と同様になりますので、詳しくは次の記事を参照ください。

MAX関数 -日付や時刻の平均値も算出できる- DL可

Excelの表計算を行う際に必要不可欠な関数の一つであるMAX関数。この関数は、引数として指定された数値の中から最大値を取得することができます。本記事では、MAX関数の基…

データ分析ドットコム

「数値」「論理値」「空白セル」「文字列」が引数のMAXA関数の戻り値

MAX関数と同様に、C列のMAXA関数の戻り値を確認してみましょう。

整理すると、次のようになります。

論理値TRUEは１、それ以外は０という戻り値になっています。

これがどんな問題を引き起こすのかを見ていきましょう。

「数値」「論理値」「空白セル」「文字列」を混在した引数のMAXA関数の計算結果

見方はMAX関数と同様です。

行3「文字列」／行4「空白セル」の場合は、いずれも最大値は0、
（行3「文字列」／行4「空白セル」は数値0に変換されるため、A列の – 1よりによりも大きくなってしまうため）

行2「論理値TRUE」は最大値は1
（行2「論理値TRUE」は数値1に変換されるため、A列の – 1よりによりも大きくなってしまうため）

という結果がC列に返ってきています。

MAX関数の0は見かけ上0ではなく、MAXA関数は見かけ上ではなく、計算対象になっている点が分かります。

したがって、

MAXA関数は、 ‘論理値’、 ‘文字列’、および ‘空白のセル’の戻り値を計算の一部として考慮する性質があります。

MAX関数とMAXA関数の性質の違いの整理

MAX関数とMAXA関数の性質の違いを整理します。

次の関係が成り立ちます。
（2016以降のバージョンのExcelが前提条件）

MAX関数を使うべき理由

MAXA関数は危険であり、その理由は次の通りにあります。

MAXA関数では、「論理値」「文字列」「空白セル」が数値変換され、計算されます。
例えば、論理値TRUEは１に変換されます。

これは避けるべきケースです。
したがって、私はMAXA関数の使用をお勧めしません。

それでも、MAXA関数を使うときの注意点

万が一、「論理値」「文字列」「空白セル」も数値変換して比較したいというケースもあるかもしれません
(通常の数値と論理値を比較するのは推奨できません)

それでも、論理値TRUE=1、論理値FALSE=0のように、どの数値に変換するかは、データ設計によって変わります。

しかし、

その場合は、「数値変換した列をもう１列追加し、データ定義書の作成を推奨します。
例えば、次のような定義書を作成し、実際のローデータに追加する形を取ります。

その際、論理値TRUE=1、論理値FALSE=0でいいかは、別途、社内外の協議をする必要があります。
もしかしたら、TUREになるケースが稀であることから、論理値TRUEは5の方が良いかもしれません。

まとめ

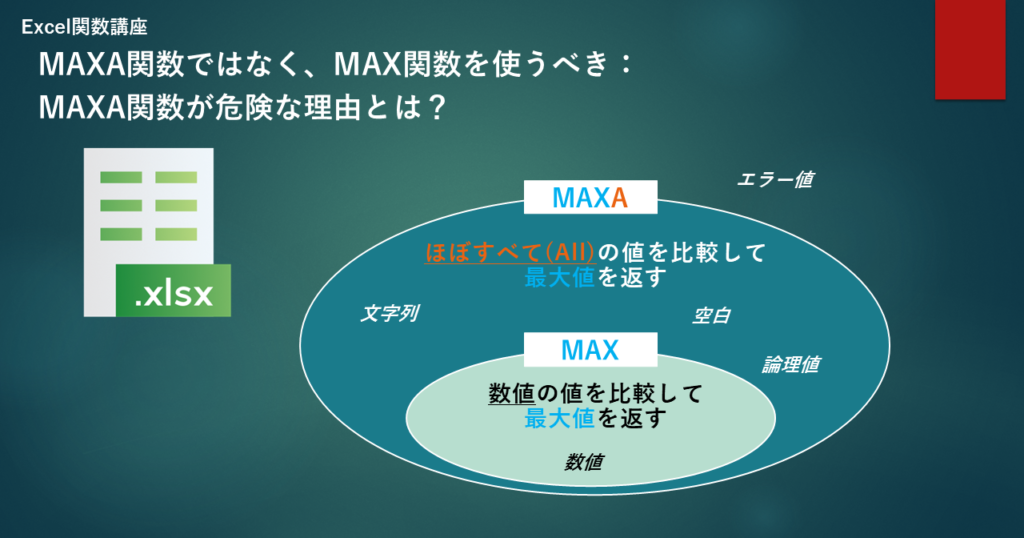
Excelの関数であるMAXA関数とMAX関数の違いについて解説しています。
MAX関数は、数値の中で最大値を求める関数であり、文字列、論理値、空白のセルは計算対象外となります。

一方、MAXA関数は、数値、文字列、論理値、空白のセルを計算対象として扱います。
そのため、MAXA関数を使うと文字列が計算に含まれてしまい、計算結果に誤りが生じる可能性があります。

データ分析ドットコムでは、MAXA関数の使用は避け、MAX関数を使用することを推奨します。

即利用できるダウンロードファイル

以下のリンクから、本記事で示したExcel MAX関数とMAXA関数をExcelファイルをダウンロードすることができます。

参考記事

関連記事

MAX関数 -日付や時刻の平均値も算出できる- DL可

Excelの表計算を行う際に必要不可欠な関数の一つであるMAX関数。この関数は、引数として指定された数値の中から最大値を取得することができます。本記事では、MAX関数の基…

データ分析ドットコム

Excel関数の原理原則

本記事の読みやすさをさらに向上させるために、Excel関数に関する原理原則についてまとめた記事を紹介します。

数式の原則｜Excel関数を学ぶ前に

Excelほど、馴染みがあり、広く浸透しているツールもないでしょう。 さらに、Excel関数はExcel作業を便利するパッケージであり、習得することで、大きな進歩につながりま…

データ分析ドットコム

数式の原則｜Excel関数の種類は大まかに知っておこう

冷静に、スムーズに仕事ができるため、Excel関数の種類を大まかに知っておくことが大切です。 Excel 2019では、Excel関数が全486関数もありますが、Excel機能を上手に活用…

データ分析ドットコム

数式の原則｜Excel関数にはそれぞれ構文がある

Excel関数には構文があります。それが、引数と戻り値です。構文に沿えばいいだけです。言わば、数学の公式のようなものです。理論を知らなくても、公式に当てはめれば答え…

データ分析ドットコム

数式の原則｜Excel関数の引数とは

Excelの引数は、料理を完成させるための材料のようなものです。しかも、材料に種類があります。その種類を理解すると、Excel関数を上手く使いこなせるようになります。

データ分析ドットコム

数式の原則｜Excelの検索ダイアログから、関数を探す

Excelの検索ダイアログに使えば、目的の関数を発見しやすくなります。WEB検索する前に、Excel関数の検索ダイアログを使ってみましょう。

データ分析ドットコム